12. December 2019
An Introduction to Skill Ratings and Match-Making in Competitive Games
Any game that has a competitive element will face the problem of how to select the right opponent for a player. This does not only apply to video games. Chess, Tennis, Champions League etc. all apply varying methods of measuring the “skill” of a player or team and aim to provide a good match.
The goals can be different. In tennis, for example, it is more exciting to see a final match of Federer against Nadal rather than seeing them face off in the first round. In chess, a game of pure skill, you want to have a worthy opponent for an interesting match. The alternative would be a match in which you beat your opponent in 10 moves – or vice versa.
The problem then is: how do I measure the skill of a player? There are a variety of systems that aim to do so.
Details in math aside, they all work on the same principle:
- Start by assigning a skill rating to a player.
- Estimate the probability of the player winning a match against the next opponent based on both their skill ratings.
- Measure match result.
- Correct the skill rating of both players.
The most well-know system that is also most widely used is Elo. Elo is named after it’s inventor Arpad Elo, who developed the system to improve the chess rating system. Different system and improvements have been developed, such as Glicko and TrueSkill. Math aside, the basic approach above is the same in all systems. And all have their own advantages, disadvantages, and quirks.
During this article, I will focus on Elo given its widespread and ease of use. I’ll go through many different aspects to keep in mind when dealing with skill rating and match-making in video-games. As a pre-amble, if you are faced with having to implement a skill-rating system, I strongly suggest to start with an Elo-type system first. The reasons are simple and manifold:
- It’s easy to implement.
- It’s widely used and well understood for many different cases.
- Its outcomes are easy to understand and familiar to players.
- Most edge cases won’t matter for your game at the start.
- It creates a great baseline from which you then can develop a more sophisticated skill-rating system if and when it’s needed.
In short: start with a well-known, predictable, and safe baseline first; worry about the edge cases later. Elo has worked just fine for games as big as Clash of Clans, Overwatch, or Clash Royale for years now. Don’t get caught up in the fine technicalities. It’s much more important to design a system that fits your desired game experience first. As you will see in the following, there is much more to that than math.
As such, this article also is not about the math details (logistics distributions, Bayes, convergence etc.). Ask your trusted Data Scientist or Economy Designer if you need those :). This article is rather aimed at game makers wanting to understand the various cases and what it means for your game.
The Elo Rating System – How Does It Work?
We assume for the basic calculation that we have two players facing off. Player A has a skill score T(A). Player B has a skill score of T(B). The basic calculation then proceeds as follows:
- Calculate the probability E(A) of player A winning when attacking player B, based on their current skill scores T(A) and T(B):
- E(A) = 1 / (1+10^((T(B)-T(A)/400))
- The probability of B winning is simply the inverse.
- Calculate the maximum score player A can win, W(A) as follows:
- W(A) = k (S(A) - E(A)),
- where if player A wins and if he loses. All skill score values are always rounded down to the closest integer. We will talk about the constant factor k a bit.
- Calculate the trophy win/loss for players A and B after the battle is over:
- After the match is over the result from 2) above is added to the skill score of player A and subtracted from the skill score of player B at the same time.
- Elo is always a zero-sum game: what you win, the other player loses.
Note that the calculation in 2) already gives the right sign (+/-) for win/loss. Let’s do an example calculation:
- Player A has a skill score of 300 and attacks player B who has a skill score of 500.
- Probability of player A winning is: E(A) = 1 / (1 + 10^((500-300)/400)) ≈ 0.25
- The score Player A can win (S(A)=1) is: W(A) = 40 (1 - 0.25) = 30
- The score the Player can lose is (S(A)=0): W(A) = 40 (0 - 0.25) = -10
If player A wins, his new score will be 300+30=330 and player B’s new score will be 500-30=470.
If player B wins, his new score will be 300-10=290 and player B’s new score will be 500+10=510.
Draws
What if the match ends in a draw? It really depends on what you want the experience to be.
In the application of Elo to chess, a draw is usually taken as “half a win, half a loss”. That means that S(A) = 0.5 for the formulas above. Note that in this case the player with the higher skill rating (Player B in our example) before the match will actually lose some score even in a draw. Inversely, player A would win that score amount for the draw. The reason is simple: as the higher rated player, player B was expected to win. Failing to do so thus adjusts his rating slightly down. Less so than for a loss, but half as much nonetheless.
However, the choice is yours. For example, in Clash Royale, which applies Elo to its trophy system, a draw gives 0 Trophies to both players. Basically, a draw does not count. If I had to guess at their reasoning for that choice, I would assume it’s simply easier to understand for players and more in line with players' expectations. This is also a good example where math takes a step back: not counting draws will make the score rating of a player converge less slowly to his “true” skill rating. Experience trumps math, however.
Whether you apply chess rules or Clash Royale’s approach is thus up to you.
As a rule of thumb: if draw’s are rather rare compared to win/lose scenarios, I would go with “draws don’t count” approach. If they are not rare, I would first consider whether having frequent draws is really the desired experience you want for your competitive game in the first place. After all, we play competitive games because we want to win.
Initial Skill Rating and Training Phases
What skill score do you give a new player? The problem is that you do not know their skill. Moreover, they most likely do not even know all the game rules yet when they start. This is, however, mostly a philosophical problem. Given that you don’t know their score, it’s fine to just assign a number and let the Elo algorithm self-correct the score by playing matches. That’s the beauty of it.
Some games actually circumvent this by having players first play a couple of training matches. In these matches, players don’t yet win/lose score points. The training matches are used to determine their initial score rating. However, this is purely player facing. For the algorithm to work, you need to assign an initial skill rating, whether you show it to a player or not.
So, which score should we apply?
If you choose to use a training phase for players (i.e., their skill rating is hidden from them for a few matches), I would suggest to start with a value of about 400. The reasons are simple. Elo is designed so that a player with score that is 400 higher than his opponent is supposed to win 91% of the time. Setting it at around 400 thus covers most cases up and down the scale and a few matches will quickly bring their score close enough to their true initial skill level. It’s not advisable to set their initial skill rating too high though. You don’t want players to start off losing the first 10 matches just to bring them down to their true skill rating. It’s a bad experience, especially at the start.
If you start showing the skill score right away, such as in Clash of Clans or Clash Royale, then I would strongly suggest to just start at a skill rating of “0”. You can even give some skill rating for tutorial matches to bring this somewhat above 0 in the first few minutes. Note that if you start at 0, then you might have to violate the “zero-sum game” rule of Elo slightly: if a player who has a skill rating of 20 is supposed to lose 30 skill points, his skill rating shouldn’t drop to “-10”. But again, those cases can usually be circumvented easily by having a few tutorial matches against bots that quickly raise the skill score to around ~100.
Rating Sensitivity and k-Factor
The “k-factor” in the formulas above plays an important rule. Basically, it dictates by how much the skill rating gets adjusted after a win/loss. For example, if you choose a k-factor of k = 60 and both players have the same score before the match, a win/loss will add/subtract exactly k/2=30 points.
In the beginning, as all good and bad players are lumped together at low initial score, you ideally want this to be high so that players get to their true skill rating quickly. However, at the top level of players, a high k-factor can be perceived as very punishing. With just a few bad matches, your top score can dwindle down vary rapidly!
In chess, the k-factor thus typically is higher for lower skill ratings and then successively gets smaller for higher skill ratings. Chess, however, is a game of pure skill. Most video games are not. For a video game, designers mostly choose a fixed value of k and stick with it.
Good starting-point references of k-factors for different games:
- Chess: from 32 for weaker players with low ratings to 16 for master players, depending on association.
- Clash Royale: 60
- Clash of Clans: 60
- World Football Elo Ratings:
- 60 for World Cup finals;
- 50 for continental championship finals and major intercontinental tournaments;
- 40 for World Cup and continental qualifiers and major tournaments;
- 30 for all other tournaments;
- 20 for friendly matches.
So a typical range would be between 20-60. The best course of action is to pick one value from a reference that best fits your game design.
Luck vs. Skill and the k-Factor
Elo was developed for chess, a pure skill game. What about luck in other games? In Clash Royale, the deck of your opponent might be very hard for you to beat with your own deck, no matter how good you are. Or a stray unit might just have been 1 pixel outside that carefully placed zap range and destroys your tower. Or in Mario Kart, you just might pick up 10 bananas from the loot boxes instead of that red turtle you wanted so badly to win the race.
As a rule of thumb, the more luck can influence the result of the game, the lower the k-factor. If the k-factor is very high, players feel very punished by losing a lot of score by being unlucky in 2-3 matches in a row.
If you are an avid Clash Royale player like me, you likely noticed this too: it’s very easy to fluctuate in your trophy score by as much as +/-200 even for players well above 4000 trophies! Such a behavior is far from ideal. First off, such as oscillating score clearly is not a very accurate reflection of a player’s true skill. Second, it’s frustrating.
I would therefore suggest to keep k a bit lower if you have a lot of random elements (such as in Mario Kart or decks in Clash Royale) that can decide or predetermine a match. Not too small though as the smallest k-factors are best applied in pure and high skill scenarios.
There is another force at work here: imagine a pure luck game, say Slots. If you made this into a competitive game where skill has no influence, all games will be played out by chance with a 50/50 win/lose rate on average. So if the k-factor is very small, the ranking distribution of players will be very narrowly centered around the average with little differences between players, which is undesirable for them. That said, the question of course is whether fully luck-driven games should apply a skill-rating system in the first place…
So why did Clash Royale choose such a high k = 60, you may ask? Obviously, I don’t know for sure. My guess is simple though: because Clash of Clans players were immediately familiar with the same trophy system and trophy ranges (Clash of Clans also uses Elo with a k-factor of 60).
Again, the right experience trumps “math”. But unless you are also building a game on top of a massively successful billion-dollar franchise that already has a well-established skill rating system in place, I suggest to keep k a bit smaller.
The World Football Elo Ratings example in the list above is also a great example of applying a different weight depending on the (perceived or real) importance of an event. This can definitely be applied for video games.
For example, different competitive modes or live-ops events such as high-profile tournaments might be connected to a higher k-factor. But the casual game played on your commute back from home has less impact on your skill rating. It just needs to be transparent to players, but it can be a great way for players to self-select just how much or how serious they want to compete vs “just play” at any given moment.
Extensions of Elo to Team-based or Massive-Multiplayer Gameplay
Elo as such is devised for a 1vs1 match, but it has also been applied to team-based sports and games. A full review of that is way beyond a simple blog post; it’s an endless topic with no single right answer. Instead, let’s focus on some basic aspects and the simplest approach for this.
The preamble above also works here: starting with such a simple approach might be better before getting lost in details you cannot fully foresee yet, especially when the game design during development is still in flux. Don’t just jump onto e.g. TrueSkill until you really have a strong grip on your game.
First, the most important questions is: who or what are trying to rate? The team or the individual player? Or both? The former is easy: two teams facing off each other can be rated just as individual players in a 1v1 game. In most video games however, individual players care first and foremost about their individual skill.
The simplest case
The simplest approach to this is as follows:
- Sum up the ELO score of all players in Team A.
- Sum up the ELO score of all players in Team B.
- Calculate the percentage of each players contribution to this total team ELO score.
- Calculate (as above) the probability of Team A winning/losing against Team B.
- Measure the result of the match
- Calculate how much score each team wins/loses.
- Adjust up/down each player’s win/loss based on their relative weight in their team.
This way you keep the simplicity of the basic ELO and just adjust how much skill rating individual players win/lose based on their weight in their team. A strong player with a score above the average of the team will hence win/lose more skill ratings points than a weak player. After all, wasn’t he supposed to be the best who can carry the team?
You might argue immediately, that this could punish the really good players if they get randomly paired up with very bad ones. The first remedy to this is to simply narrow the Elo Rating range in which you match-make team-members together. That way, the game designer a priori controls how big the skill difference can be.
Nevertheless, if you google “Elo Hell”, this scenario can be a pain-point for players, whether it’s real (not really) or not. Given this stigma of “Elo hell” even for long-running top games like League of Legends, it seems much more a problem of players' perception, not a problem of “fair math”. The term “Elo Hell” is also used independent on whether or not the actual skill rating system used is Elo, Glicko, or TrueSkill. It’s a design and experience problem, not a problem of the “right math” or system.
More complicated scenarios and undesirable side-effects
Wrong and the right incentives
The most common alteration to the simple case above is to keep track of the individual’s performance during a match. Here is a good reference for a simplified game of two teams shooting basketball free throws against each other. In this example, there actually is a clear and unambiguous measure of the accuracy (and hence skill) or a player. But what about a game like Overwatch? Or League of Legends? What would be a good measure?
For simple shooters, one might argue that the Kill/Death ratio might be a good metric of a player’s skill. However, what if you are playing deliberately a support character such as as healer in Overwatch? You’re not going to get a lot of kills… What’s worse, you might incentivize the wrong behavior in players. Player’s care a lot about their skill rating, especially if it can be seen easily by other players. Scoring them by their K/D-ratio might incentivize them to protect that score more so than winning the match for their team.
As a real word example, Overwatch actually removed “Personal Performance Skill Rating Adjustments” from the skill ratings in Season 8. To quote: “we want players to not be distracted and worry about how to optimize around the personal performance adjustment. They should just be trying to WIN.”
So be mindful of “overdoing” improvements on the above simple case scenario too soon. Start simple, look for references and how they deal with it, listen to players and then adjust the algorithm step by step. Also, instead of only focussing on individual player’s performance/skill, don’t forget other factors and behavior that you can and should reward or punish:
- Players quitting matches often prematurely.
- Players experience/tenure in the game.
- Membership in the same clan/squad when joining a match
- …
Overall, the most important question to ask and answer what experience you want. For individual players, the individual rating score might be most important. But if your game is exclusively team-based, then the “skill” of a player should mostly be a measure of how much he contributes to his team actually winning matches, not some individual performance feat. Lionel Messi might be the best footballer in the world – but would it really matter if he scored a 100 goals each season but FC Barcelona does not win a single title? I’d say no.
Mario Kart: Good math but potentially confusing experience
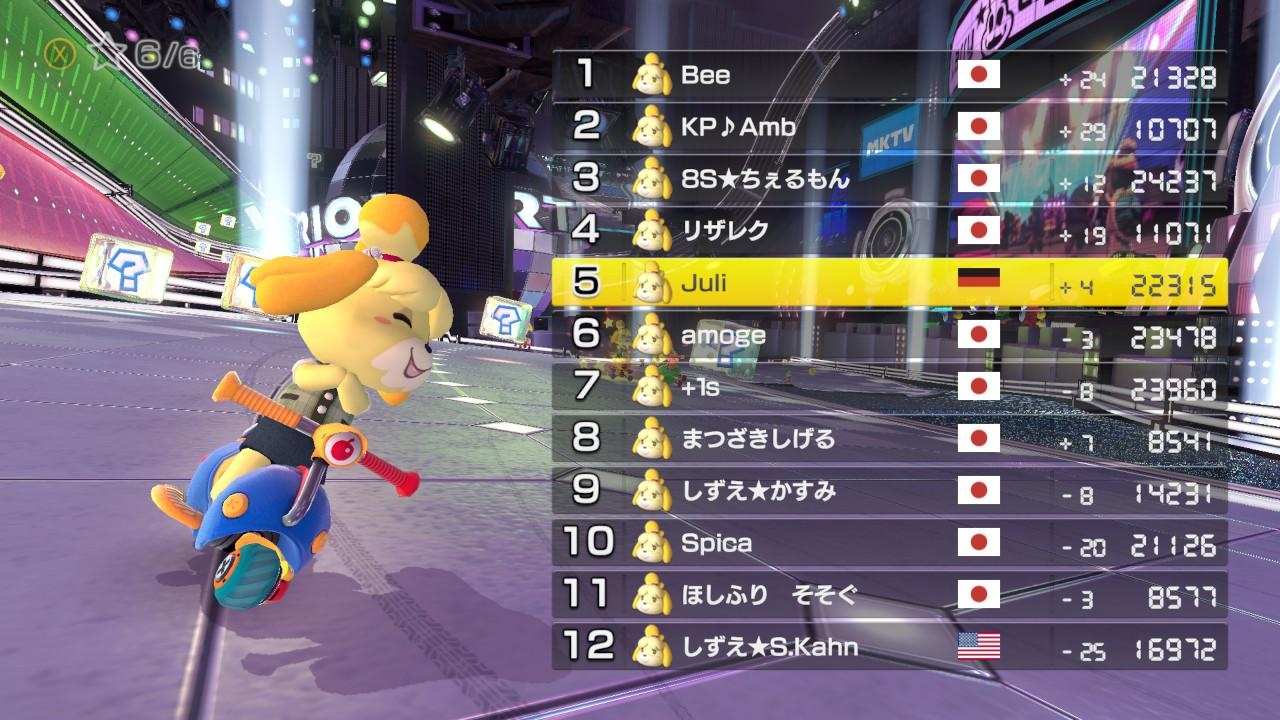
Below you can see the results screen of an online competitive Mario Kart race:
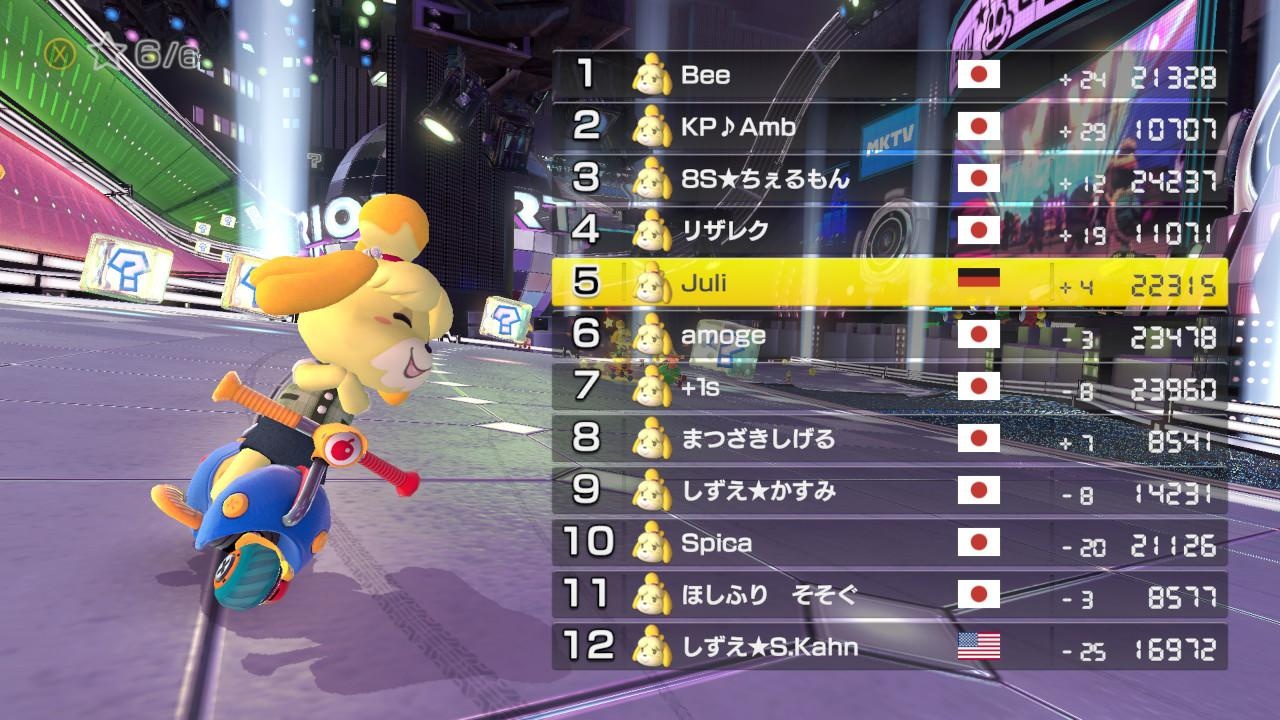
Notice something? The number 6 and 7 in the results lose skill rating, while the player in position 8 wins some rating points. From a pure system point of view, this is logical if you look are the current skill ratings. Players 6+7 have ratings >20k points, whereas player 8 only has a rating around 8500. So Player 8 clearly over-performed vs. his opponents, whereas players 6+7 were expected to have better results.
Nevertheless, it can be hard and confusing for players to understand in the moment. Imagine Lewis Hamilton losing championship points in Formula 1 if he finished in 7th place behind opponents who are rated worse drivers. From a pure Elo-type of thinking, Mario Kart makes sense: the game basically does a pairwise comparison of all match-ups in the roster and then adjusts the default points given for each position in the final results table. So theoretically, you can be second to last in the race and still win points if the other players where rated much higher than you. But context matters too.
How to deal with such cases is again more a question of game design rather than “the right model”. Maybe Mario Kart would do better by keeping track of the skill-rating in the background and use it for good match-making while showing players a simpler trophy score like Formula 1 which resets regularly. Then again, maybe not. The choice ultimately is a creative one and the system needs to adjust to the vision of the game.
In the Mario Kart case, I personally find the current system and experience not very great, not the least because Mario Kart does have a lot of intentional and fun randomness built deeply into the core gameplay. Even the best of players can get caught by a nasty blue shell in the last turns of the last lap and end up finishing 4th despite having lead the race from the start till that point.
What about Fornite & Co?
As far as I could find out, Fortnite does not apply any skill rating for match-making. In a 100p all-against-all scenario, the outcome is highly unpredictable. In other words: skill would not be a very good predictor for who is going to win in the first place.
On the flip side, it also already takes quite a while to get 100p together to get a match started – adding a layer of skill-based match-making on top would only increase this time.
More reading on team-based skill-rating
- Some more insight and a great starting point for more research into the topic is Microsoft’s paper on the TrueSkill2 algorithm.
- Overwatch post on “Limiting the Skill Rating variance for Teams”
- “Adapting Elo for Relative Player Ranking in Team-Based Games”
- Nice breakdown and resources for implementing TrueSkill
- The World Football Elo Ratings
- Overwatch’s Game Director Jeff Kaplan on match-making. Great reminder of the importance of match-making time and ping as well as the inevitability of real/perceived “unfair” matches and results.
Basics of Skill-based Match-Making
Ok, now we have a game in which players compete and way to keep track of their current skill rating. How do we then select suitable opponents for match-making?
Before we start, keep in mind two things:
- in real world match-making, skill is only one important ingredient. But other factors, most notably match-making time, connection stability, speed, and latency are crucial! Don’t forget about them!
- Different mode, different skill: If you game has different games modes (such as e.g. Team Death-match and Capture the Flag in a FPS), you should keep in mind that players may be better or worse in different modes.
Good competitive games should feel “fair” to players. So the simple approach is to look for opponents with the same skill rating. However, few players in the world are likely to have the exact same skill rating as you. Instead, the game will look within a skill-rating range around the players score for opponents.
So how big should this range be? Basically, you want a player to have a reasonable chance to win. You can use the Excel I attached above to get a feeling for those ranges. Let’s look at some examples:
| Score rating Player A | Score Rating Player B | Win probability for Player A |
|---|---|---|
| 1000 | 400 | 97% |
| 1000 | 800 | 76% |
| 1000 | 900 | 64% |
| 1000 | 1000 | 50% |
| 1000 | 1100 | 36% |
| 1000 | 1200 | 24% |
| 1000 | 1600 | 3.1% |
Roughly speaking, a range of +/-200 might still be considered acceptable. However, apart from matching the perfectly skilled partner, match-making time is often even more crucial to players. Especially in a real-time PvP game, it might be hard to find a player who has a similar skill rating, who is also currently online playing, and also looking for a match in the queue right now. So in reality, you need to strike a balance.
Rather than just sticking to fixed ranges, it may also make sense to this a bit smarter with a simple algorithm that quickly balances the time-to-wait for a match with the right skill score range:
- Check how many players within +/-20 skill score points are online right now.
- Estimate the time before one becomes available for a match (not hard to estimate)
- If (estimated time) > (acceptable waiting time), increase search radius to +/-40
- Rinse & Repeat until you find a match within acceptable time range.
This highlights another problem you may face: match-making high-ranked players. If you look at a typical player rating distribution for Chess, it looks like this (taken from Lichess):
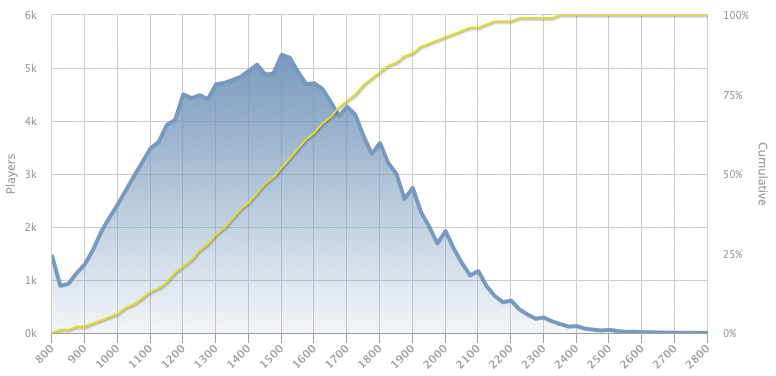
Note how you have more than 5000 players around a skill rating of 1500? However, at a skill rating of 2600, you only find twelve players. This is obviously a problem. Luckily (pun intended), most video games are not games of pure skill. This usually allows you to get away with a wider match-making range. It’s also general problem of any competitive ranking system. After all, how many players in the world of Tennis are likely to beat Roger Federer in a match?
What this highlights though is that it’s important to be flexible enough in the skill-range used for match-making, so that players find a the best possible match within a reasonable waiting time.
None of this is really a big issue if you player base is really large. For example, experience tells us that in Clash Royale, it’s virtually impossible to ever win/lose more than 24 trophies in a match (the average being 30 based on the k-factor of 60). You can easily calculate that their match-making range is within +/- 70 trophies for this particular game.
Skill Rating as a Progression Scale
By now it is (I hope) clear that it is essential to keep track of players' score in competitive games. Equipped with it, you keep track of how well players perform and how to best select players for the right match-ups based on their skill.
However, this does not mean that you have to show players this skill rating in your game. It’s a design choice. Some games do not show it and it just runs in the background, unknown to players. This might be useful if your game is structured around seasons or regular tournaments, in which players score points or climb rankings. These seasonal or tournament rankings can easily be reset once the season/tournament is over. Their skill rating, however, stays the same!
Other games, such as e.g. Clash of Clans and Clash Royale, have made the skill rating a corner stone of the progression system. In Clash Royale, “Trophies” = your Elo skill rating in the game. As players get better they increase their trophy count and progress through different “Arenas” which are just another, higher band of skill-rating.
Such a system can, as Clash games show, work really well. But you should make a very conscious choice here since skill ratings are truly based on the current results and it is not something that you can easily change post-hoc or control a priori. This brings us to the next point: power progression and what I call “Elo creep”. Let’s talk about that one.
Games with Power Progression: Skill-vs-Power and “Elo Creep”
Above we talked the influence of “random luck”. What about games that allow you to get more powerful? Such as getting a more powerful car in a racing game, or making your Hero more powerful in a MOBA, or getting stronger units in a battle-strategy game?
The beauty of such skill rating systems is that they are constantly self-correcting. So if your game allows power progression, then your current skill rating reflects the mix of your skill given your current power. In other words: if Player A and B both have a power (or level) of, say “20” for their Hero, their skill might be very different. If Player A is the much better player, then his final skill rating will be higher than that of Player B even though they have the same power.
Power progression also leads “Elo Creep”. Basically, it means that your skill rating will creep to higher and higher numbers as you power-progress through the game, regardless of whether or not you are actually getting better, i.e., increase your skill. Clash of Clans is a particularly good example: you do not even need to attack other players. If all you do is build and upgrade your base, your Elo rating (Trophy count) will creep up just because players that attack are more likely to lose when your base gets stronger.
The important thing though is that, ultimately, these factors are self-correcting with respect to where it matters: match-making. The important thing is to provide players with good, fair, and interesting match-ups and the skill-rating score will do just that, including both power and skill implicitly. It may lead to situations in which players can get frustrated because they lose against a much more powerful opponent (looking at you, Clash Royale!) – but the inverse is also true. Players will also win matches against more powerful opponents simply because of their skill – and winning as the “underdog” does feel good too.
Rating Decay and Seasonal Rating Resets
Once many matches are played, the skill ratings (ideally) converge on the true skill of a player. So consider that you are the top-rated player in a game. Why would you even want to play a game? Given that your rating is higher than anyone else’s, you have more to lose than to gain. In such cases the rating system can discourage game activity for players who wish to protect their rating.
There are two ways of dealing with that: rating decays or seasonal resets.
Rating decay
Many games apply such a system for players above a certain high-skill threshold. Beyond that threshold, skill ratings points will decay after a fixed amount of time. An example:
- We decide to apply rating decay to all players above a rating of 4000.
- Player A starts at 4000 and plays a great match, reaching a new skill level of 4035.
- However, these +35 skill points will decay (i.e., removed) after 1w.
- So if Player does not play any further matches in one, his skill rating will drop down to 4000 again.
Obviously, the rate of decay could also be gradual as well as have different timings. This really depends on the desired experience and game design.
Seasonal Resets
In many ways, this is a variant of rating decay. But rather than keeping track of all individual scores and their decay time, the game resets all ratings above a certain threshold back to the threshold. This might be easier to keep track of and it’s easier to communicate to players. However, if your game does not have any clear seasonal-type meta, it might be the worse choice.
Clash Royale started doing these types of seasonal resets for Trophy Scores >4000 last year. After the first few resets, they added a twist though: rather than resetting all players back to 4000, the trophy amount above 4000 gets halved. The reason for this was match-making: the top-skilled players have skill ratings well-above 6000 at the end of a season. Resetting everyone back to 4000 will lead to a lot of poor match-ups right after the reset until. This is neither fun for the top players nor for the ones that get beaten badly.
Both system, rating decays and seasonal resets, can also be mixed together. The main question is again around the creative vision: what experience do you want for your player audience? The purpose of decay and resets is simple: you want to keep the race to the top going and fresh for a long time.
The game and leaderboard at the top should never get static and boring. And simply not playing to protect your rating should not be rewarded for too long.
Adjusting score based on the result of the match
Chess is a simple win/draw/lose game. There is no scoring involved. Now consider a football match between Brazil and Germany: would you rate a friendly match result of 1:0 in the same way as a 7:1 beating in the World-Cup semi-finals? Maybe not.
So do we adjust the skill rating based on the score? Let me give you two examples where this is done in a nice an easy way.
Clash of Clans Trophy results based on Stars won
Clash of Clans applies a simple ELO system with a k-factor of 60. So if you attack and win against a player with the same trophy count, you’d expect to win 30 trophies. However, Clash of Clans only awards the full amount if you win the battle with the full 3 Stars. Stars are given for
- Destroying the enemy HQ
- Destroy more than 50% of the base and
- Destroy the entire base.
For each star that you fail to win, the trophy reward is reduced by 1/3. So in our example, if you win with 1 Star, you will be awarded 10 Trophies; if you win with 2 Stars, you will be awarded 20.
In basic terms: the k-factor is reduced by 1/3 for each Star you fail to win.
The World Football Elo Ratings based on score difference
FIFA applies Elo to their ranking of national teams. Apart from the different k-factors depending on the importance of match (e.g. World Cup final round vs friendly matches), they also apply an increase to the k-factor depending on the score difference:
- It is increased by half if a game is won by two goals;
- by 3/4 if a game is won by three goals;
- and by 3/4 + (N-3)/8 if the game is won by four or more goals, where N is the goal difference.
So theoretically, a team can win up to twice as many skill ratings points for a very lopsided win. Personally, I prefer this approach over the one used in Clash of Clans, for a couple of reasons:
- It feels nicer to get a reward for achieving well than feeling punished for “only” getting 1 star.
- It incentivizes attack win over pure defense win, which I believe is more fun for most players – and watchers of the sport.
- It will reduce “Elo creep” issues: good skilled attack will win you more than losing against a tanking, much more powerful opponent.
When not to Use Elo-Type Systems
There a two scenarios I can think where an ELO type system (ELO, Glicko, or TrueSkill variants) may not be appropriate:
- Tournament driven games
- Pure luck games
I discussed pure luck games already above. Basically, if the game is pure lock (like a coin toss), then your “skill” rating will just be determined by random chance.
The second case is best explained with the example of Tennis and the ATP rankings: on the ATP tour, players score points towards their rankings based on their results in tournaments. The ATP then decides two things:
- which tournaments to include for ranked matches;
- the weight of each tournament.
For example, winning a Grand Slam tournament such as Wimbledon will award the winner with 2000 points towards the ranking, while reaching the finals will award 1200 points. Reaching the Quarterfinals still awards 360 points. Winning a master series tournament, on the other hand, will “only” awards 1000 points to the winner.
In addition, the ATP applies decay to the points: only the points awarded to a player over the past 365 days running are counted. So if Roger Federer retires tomorrow, you would slowly see him dropping out of the Top 10, the Top 100 and the rankings altogether over time. In a nutshell, the player winning the most and the most important tournaments (or reaching at least on average the farthest on average) will sit in the #1 spot of the rankings, just as any watcher of the sport would intuitively expect.
Such a system is very appealing when the meta of a game is based mostly around “Tournaments”. One could also imagine how such a system could be applied easy to Battle Royale type of games such as Fortnite. If Fortnite introduced “Ranked” matches, such a system would award points based on how long players survived, with most points going to final winner. In turn, it seems impractical to try and apply an Elo type skill rating to players in Fortnite.
Final thoughts
Skill ratings for players may seem very daunting and complicated. But I hope you can see that it follows some basic principles and rules that you can apply to many types of competitive games.
In the end, the first and foremost question is one of creative direction: what type of game and what type of experience do you want for your players? Start there and then decide, which system to apply and how to apply it best for your game.
Keep in mind the rule of thumb to start with the simplest, most well-known, and familiar system for players for a given situation first. Don’t get lost in forum flamewars about which system is “best”.
Just like the chosen programming language ultimately won’t decide the success or failure of game, the choice of skill ranking system won’t be the single deciding factor. Keep it simple first, then figure out which variations, such as decay, resets, score rewards, team-based rating rules etc. you really really need.
I work for King. All views in this post are personal and my own. They do not represent the views of King or ActivisionBlizzard.